Порядок и процедуры кинематического анализа

В ходе кинематического анализа расчётной схемы сооружения даются ответы на два главных вопроса:

1) достаточно ли суммарное число внешних и внутренних связей в системе для того, чтобы при правильном их размещении обеспечить её геометрическую неизменяемость?

2) правильно ли расставлены связи?

Следует обратить внимание на то, что первый вопрос ещё не предполагает изучения правильности расстановки связей – он  нацелен на оценку их количества.

В связи с этим в кинематическом анализе выделяются два последовательных этапа:

1) количественный анализ;

2) качественный (структурный) анализ.

Количественный анализ

К о л и ч е с т в е н н ы й   а н а л и з – это исследование расчётной схемы сооружения, заключающееся в оценке баланса    (соотношения) суммарного числа степеней свободы дисков системы до наложения на них внешних и внутренних связей (т.е. несвязанных дисков) и суммарного числа внешних и внутренних связей системы,  в пересчёте на связи первого типа.

Указанный пересчёт объясняется тем, что именно связь первого типа способна устранять, при правильном её использовании, одно возможное взаимное перемещение (линейное или угловое) соединяемых дисков, т.е. одну степень свободы.

Количественная оценка степеней свободы и числа связей

Суммарное число степеней свободы несвязанных дисков системы обозначим , а суммарное число условных (в пересчёте) связей  первого типа –  n_c.

Для правильной оценки соотношения между  и n_c  (больше, меньше, равны) необходимо, изучив расчётную схему сооружения,  заранее строго определить, какие элементы системы считать дисками, а какие рассматривать как связи. При этом имеет смысл учитывать возможности, проиллюстрированные выше на рис. 1.25. Один и тот же элемент не может одновременно быть и  диском, и  связью; связи должны налагаться только на диски, но не друг на друга.

После номинации дисков выполняется формальное выявление внешних и внутренних связей в системе по следующему алгоритму:

1) определяются  возможные комбинации  соединений дисков друг с другом, исключая диск «земля» (например, четыре диска системы D₁ , D₂ , D₃ , D₄   могут иметь соединения в следующих шести сочетаниях:  D₁D₂ , D₁D₃ , D₁D₄ , D₂D₃ , D₂D₄ , D₃D₄ );

2) каждая  комбинация  проверяется  на  предмет реального существования предсказанных в главе 1.3 возможных соединений соответствующих дисков, и в случае наличия связей (одной или нескольких) определяются их типы;

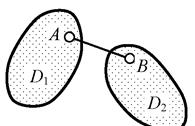
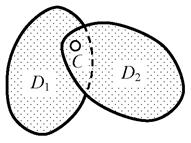
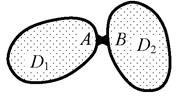
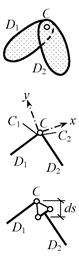
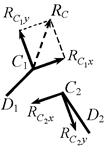
        3) дополнительно для всех дисков проверяется  наличие связей между точками   одного  и  того  же  диска (примеры  –  на рис. 1.29:  связь  3-го типа (припайка)  в  узле А  диска D₁ (криволинейного стержня с замкнутой осью), связь 2-го типа (шарнир) в диске-стержне D₂  и связь АВ 1-го типа (линейная) в диске D_3 ;

        4) во всех точках,  где имеются соединения  с  диском «земля» (опоры), т.е. внешние связи, оцениваются их типы и подсчитывается число эквивалентных им связей 1-го типа.

Число дисков системы (без учёта диска «земля») обозначим D, число внутренних связей 1-го типа – С, 2-го типа (шарниров в плоских системах) – Н, 3-го типа (припаек) – П, суммарное число внешних связей (с диском «земля»), пересчитанных на связи 1-го типа – С_о.

Рис. 1.29

Рассмотрим примеры реализации вышеприведённого алгоритма, учитывая, что для одной и той же системы возможны различные варианты представления о её дисках и связях.

Например,  систему  с  расчётной  схемой  по  рис.1.30, а, можно  считать  состоящей  из  шести  дисков  (D₁ , D₂ ,…, D₆  на    рис.1.30, б), тогда внутренними связями являются три припайки П₁ , П₂ , П₃  между дисками D₁D₂ , D₂D₅ , D₃D₄  и три шарнира Н₁ , Н₂ ,Н₃  между дисками D₁D₆ , D₅D₆ , D₂D₃ (или D₅D₃ – альтернативно, но не одновременно с D₂D_3 !, так как диски D₂ и D₅ соединены жёстко, и в соединении с диском D₃ формально выступают как единый диск, учитываемый только один раз). Соединения с «землей» имеются в точках А, В и G, где расположены соответственно неподвижная защемляющая опора (внешняя связь 3-го типа), подвижная шарнирная опора (внешняя связь 1-го типа) и неподвижная шарнирная опора (внешняя связь 2-го типа). Суммарное число эквивалентных связей первого типа равно  3 + 1 + 2 = 6.

   

Рис. 1.30

Во втором варианте (см. рис.1.30, в) П-образная левая часть системы состоящая из трех стержней, жёстко соединенных в узлах  Р и S,  считается  диском D₁  (эту часть  также можно рассматривать просто как диск в виде стержня с ломаной осью). Аналогично назначен диск D₂ . Горизонтальный элемент KL рассматривается как диск D₃ . Формально к дискам отнесен также опорный стержень в точке В, обозначенный как диск D₄. Четыре диска соединяются друг с другом только шарнирами – их четыре (Н₃ и Н₄ – соответственно между дискамиD₁D₂ , D₁D₄   и два – Н₁ и Н₂ между D₁D₃). Опоры в точках А и G – такие же, как в первом варианте, а посредине диск D₄ имеет опорный шарнир в  точке В’. Суммарно опоры эквивалентны 3 + 2 + 2 = 7 связям первого типа.

В третьем варианте (см. рис. 1.30, г) рассматривается только один диск D₁. Поэтому внутренних связей, соединяющих его  с другими дисками, нет. Стержень KL, схема которого точно соответствует определению линейной связи согласно рис. 1.12, учитывается как внутренняя связь 1-го типа между точками K и L одного диска (в соответствии с п. 3 приведённого выше алгоритма). Правый стержень с ломаной осью отнесён к внешним связям в качестве условной линейной связи с осью SG (по аналогии с рис. 1.25, б). Внешние связи (опоры) в точках А и В – такие же, как в первом варианте. Суммарное число эквивалентных внешних связей 1-го типа: 3 + 2 + 1 = 5.

Таким образом, в трёх рассмотренных вариантах номинации дисков и связей имеем:

– по рис. 1.30, б:   D = 6,  П = 3,  H = 3,  C = 0,  C_o = 6;

– по рис. 1.30, в:   D = 4,  П = 0,  H = 4,  C = 0,  C_o = 7;

– по рис. 1.30, г:   D =  1,  П = 0,  H = 0,  C = 1,  C_o = 5.

Возможны и иные варианты представления о дисках и связях той же системы.

В некоторых точках (узлах) могут соединяться шарнирно или жёстко более двух дисков (рис. 1.31, а, б  соответственно).

Шарнирный узел (см. рис. 1.31, а) по существу  представляет собой попарное соединение дисков бесконечно близко расположенными шарнирами (см. рис. 1.31, в), условно изображаемыми с общим центром (осью вращения). Поэтому шарнир, соединяющий более двух дисков, называется кратным (или сложным).  Очевидно, что в нем объединены n_{D, уз} – 1 обычных (иногда говорят – простых) цилиндрических шарниров; здесь n_{D, уз} – количество дисков, соединяемых в узле кратным шарниром. В случае, показанном на рис. 1.31, а, соединение дисков в узле учитывается как три простых шарнира (Н_уз = n_{D, уз} – 1 = 4 – 1 = 3). Заметим, что если какой-либо стержень из сходящихся в шарнирном узле отнесён не к дискам, а к связям 1-го типа, то при подсчете кратности шарнира он, конечно, не учитывается.

Рис. 1.31

Аналогично кратной, т.е. соединяющей более двух дисков, может быть и припайка (см. рис. 1.31, б), эквивалентная также   n_{D, уз} – 1  простым  припайкам  (двум  в  узле,  изображённом  на   рис. 1.31, б:  П_уз = n_{D, уз} – 1 = 3 – 1 = 2).

Очевидно, что в случае, приведённом на рис. 1.31, г, несмотря на наличие трёх сходящихся в узле стержней, припайка не является кратной, так как два из трёх стержней заранее объединены в диск D₁. Если какой-либо из стержней, жёстко соединённых в узле, принят в качестве связи 3-го типа (в соответствии с рис. 18, в), то он не учитывается  в  n_{D, уз .}

Расчётная схема сооружения может содержать узлы, в которых осуществляется одновременное соединение дисков с помощью шарниров и припаек (например, узел S на рис. 1.30, б), в том числе и кратных. Такие узлы, в отличие от тех, где соединение дисков только шарнирное (шарнирные узлы) или только жёсткое (жёсткие узлы), называются узлами с комбинированным соединением дисков. Для правильной оценки числа эквивалентных простых шарниров и припаек требуется аккуратная оценка кинематических свойств комбинированного соединения. Например, в узле, изображённом на рис. 1.32, а, жёстко соединяются три диска-стержня D₁, D₂ и D₃  (соответственно кратная припайка эквивалентна 2 простым), а кратный шарнир связывает четыре диска – D₄ , D₅ , D₆  и объединённый диск D_I = D₁ + D₂ + D₃ и поэтому эквивалентен трём простым; следовательно, П_уз = 2,   Н_уз = 3.

Рис.1.32

В комбинированном узле, показанном на рис.1.32, б, соединяются семь дисков с помощью двух простых и одной кратной припайки, эквивалентной двум простым, а также кратного шарнира,  связывающего три укрупнённых диска D₁ + D₂ ,  D₆ + D₇  и  D₃ + D₄ + D₅ . В итоге для узла имеем П_уз = 4, Н_уз = 2.

Замечание, не имеющее прямого отношения к кинематическому анализу,но полезное в дальнейшем:

Особенности соединения нескольких элементов в шарнирном узле реальной конструкции определяются конкретным инженерным воплощением узла: возможно соосное объединение элементов на общем цилиндрическом вкладыше – в этом случае кратный шарнир в расчётной схеме появляется естественным образом; могут применяться также различные сочетания шарнирных соединений с небольшими расстояниями между осями шарниров – при формировании расчётной схемы конструкции эти малые несоосности могут игнорироваться, что опять же приводит к возникновению кратного шарнира. Каким образом появился кратный шарнир в расчётной схеме сооружения, для кинематического анализа не имеет никакого значения. Однако на стадии расчёта конструкции целесообразно конкретизировать соединение дисков в узле, обозначив определённую комбинацию простых шарниров – это позволяет составить чёткое представление о реакциях связей и о том, к каким именно соединяемым дискам те или иные из них должны быть приложены.

Разные варианты внутренней структуры сложного шарнирного узла отличаются лишь «игрой сил» в самом узле, т.е. различными комбинациями реакций связей простых шарниров. Для реальной конструкции это, несомненно, имеет значение в области узла, малой в сравнении с размерами элементов конструкции, но за пределами этой области особенности внутреннего распределения сил в ней практически не влияют на усилия в системе. Поэтому если сведения о конкретном конструктивном решении узла отсутствуют, то можно задать в нем любое соединение дисков простыми шарнирами, выбрав наиболее удобный из нескольких вариантов. Например, альтернативой модели, приведённой на рис.1.31, в,  является прикрепление диска D₄ шарниром не к D₁ , а к D₂ или D₃  (возможны и другие комбинации соединений).

После того, как выполнено разделение элементов расчётной схемы сооружения на диски и связи (NB: не должно остаться ни одного элемента, не отнесённого к одной или другой категории!), выполняется вычисление и последующее сопоставление n_ и n_c . Суммарное число степеней свободы несвязанных дисков определяется исходя из того, что каждый жёсткий пространственный диск, как установлено выше, обладает шестью степенями свободы, а плоский – тремя. Тогда если, как принято ранее, число дисков системы – D, имеем

      

При выводе формулы для суммарного числа внешних и внутренних связей n_c (в пересчёте на связи 1-го типа) учитывается, что пространственная припайка эквивалентна шести  простым связям (плоская – трём), шарниры плоских систем (цилиндрические и поступательные) учитываются как две связи 1-го типа, шаровой шарнир в пространственной системе – как три:

     

При использовании формулы ( 2 ) для пространственной системы все соединения, не подпадающие под признаки припайки, шарового шарнира или связи 1-го типа, непосредственно представляются как комбинации соответствующего числа простых связей.

Необходимое условие геометрической неизменяемости

Очевидно, что для обеспечения геометрической неизменяемости системы необходимо отсутствие возможных перемещений (степеней свободы) у её дисков после наложения на них всех выявленных внешних и внутренних связей. А это возможно лишь в том случае, когда суммарное число связей n_c не меньше суммарного числа степеней свободы  несвязанных дисков, т. е.

,                                         ( 3 )

в противном случае останутся некоторые неустраненные степени свободы, что является признаком геометрически изменяемой системы. Если ввести для характеристики соотношения  и n_c их разность

,                               ( 4 )

то условие ( 3 ) примет вид

_.                                             ( 5 )

Неравенства  ( 3 )  и  ( 5 )  выражают  необходимое, но недостаточное условие геометрической неизменяемости  системы.

Недостаточность условия неизменяемости в виде ( 3 )  или  ( 5 ) проявляется в том, что оно имеет сугубо количественный характер и не может учесть возможных дефектов в размещении связей. Не исключена ситуация,  когда характеристика W неположительная, т.е. условие (5) выполняется, но связи в системе распределены неправильно: например, с переизбытком в некоторых частях, тогда в других частях их может быть недостаточно, и там остаются некоторые степени свободы дисков. Следовательно, выполнение необходимого условия геометрической неизменяемости не гарантирует того, что система в действительности будет неизменяемой.

Результатом  проверки  выполнения условия ( 5 ) является одно из двух  альтернативных заключений:

1)  система  может быть  неизменяемой (если получено W = 0 или W < 0);

2)  система геометрически изменяема (при W > 0).

Вычисление характеристики W и проверка выполнения необходимого условия геометрической неизменяемости составляют содержание 1-го этапа кинематического анализа – количественного анализа расчётной схемы сооружения. В представленном на рис. 1.6 алгоритме кинематического анализа количественный анализ является частью процедуры проверки, обозначенной оператором 1, и обеспечивает немедленный выход из  него при W > 0 (ответ «нет»). В случаях W = 0 или W < 0 для  выхода с ответом «да» или «нет» необходимо дальнейшее исследование расчётной схемы сооружения – структурный анализ системы.

Для вычисления характеристики W служат формулы, получаемые подстановкой в ( 4 ) выражений ( 1 ) и ( 2 ):

Рассмотрим определение W для трёх вариантов описания плоской стержневой системы (см. рис. 1.30, б, в, г):

– по варианту 1: W =  

– по варианту 2: W =  

– по варианту 3: W =  

Во всех трёх вариантах получено, как и следовало ожидать, одно и то же значение W = –3 < 0. Заключение по результатам количественного анализа: система может быть геометрически неизменяемой, так как связей количественно хватает (и даже имеется некоторый их избыток), чтобы при правильном их размещении обеспечить устранение всех степеней свободы дисков системы.

Для системы, изображённой на  рис. 1.33,  после  обозначения дисков D₁ , D₂ ,…, D₅  имеем: D = 5;  П = 0;  Н = 4 (в  узлах К, L и кратный в узле G); С = 0; С_о = 7 (опорные шарниры А и С, каждый из которых эквивалентен двум связям  1-го типа,  и  неподвижная защемляющая опора В  –  три связи);

W =  – система может быть геометрически неизменяемой.

Рис.1.33

В системе, схема которой показана на рис. 1.34, выделены шесть дисков ( D = 6 ). Жёстких узлов нет ( П = 0 ). Шарниров четыре  (все  простые – соединяют  диски  попарно:  D₁D₂ , D₂D₃ , D₃D₄ , D₄D₅ ), т.е. Н = 4. Внутренние связи 1-го типа – стержни CS, SJ,TP и TL; С = 4. Внешних связей – пять (С_о = 5): стержни АС и LK, а также три связи в опорах В и G. Находим W = > 0 – система геометрически изменяемая.

Рис. 1.34

Можно стержень JР отнести не к дискам, а к внутренним линейным  связям,  тогда  D = 5,  П = 0,  H = 2,  C = 5,  С_о = 5  и   W =  >  0 – результат не изменился.

Заметим, что в обоих вариантах диск D₆ необходим, так как иначе стержень SТ должен рассматриваться как связь 1-го типа, и в узлах S и Т связи будут соединяться только друг с другом, что недопустимо.

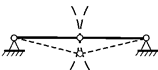
Замечание: иногда характеристику W называют числом степеней свободы системы. Использование такого не вполне корректного термина  может  стать  причиной  неверного  вывода:  ведь если вложить  в  W смысл, отвечающий названию, то результат W = 0  формально следует  истолковывать как отсутствие у системы степеней свободы  и, следовательно, оценивать систему как геометрически неизменяемую; но это не всегда  соответствует истине.  Например,  в случае,  представленном  на рис. 1.33,  W = 0, но  в  действительности существует очевидная   возможность   конечных  перемещений дисков в правой части системы (рис. 1.35), полностью определяемых углом ;  следовательно, у системы всё-таки имеется одна степень свободы. Объяснение этой ошибки заключается в том, что названием «число степеней свободы системы» характеристике W придается несвойственное ей содержание качественного характера, выводящее на заключение о кинематическом качестве системы, в то время как W служит лишь для оценки количественной достаточности или недостаточности связей для возникновения возможности устранения всех степеней свободы несвязанных дисков (вопрос о том, реализуется или нет указанная возможность, на этапе количественного анализа системы вообще не рассматривается). Некорректность термина «число степеней свободы системы» в применении к характеристике W особенно отчётливо проявляется в случае отрицательного её значения.

Рис. 1.35

Как уже отмечалось выше, если в результате выполнения 1-го этапа (количественного анализа) обнаружено, что расчётная схема системы удовлетворяет необходимому условию геометрической неизменяемости ( 5 ),  то осуществляется её качественный (структурный) анализ, представляющий собой 2-й этап кинематического анализа.

Условия геометрической неизменяемости стержневых систем

                                               Основные понятия и определения

Начинать расчёт сооружения имеет смысл лишь тогда, когда установлено, что он вообще может быть выполнен методами строительной механики, и определено, какие методы при этом следует использовать. В противном случае попытки составить и решить соответствующие уравнения могут оказаться безуспешными из-за возникновения нехарактерных для решаемой задачи математических проблем (недостаточность уравнений, их вырождение и др.). Поэтому необходима предшествующая расчёту оценка расчётной схемы рассматриваемой системы, называемая кинематическим анализом сооружения (системы).

К и н е м а т и ч е с к и й   а н а л и з – это исследование расчётной схемы сооружения (системы), выполняемое до      на­чала расчёта с целью определения кинематического качества системы (геометрической неизменяемости, мгновенной изме­няемости или геометрической изменяемости), а в случае гео­метрической неизменяемости системы – также для выявления её статической определимости или неопределимости.

Кинематический анализ позволяет своевременно обнаружить системы, расчёт которых либо вообще невозможен методами механики деформируемых тел – геометрически изменяемые системы (ГИС), либо может выполняться с использованием особых подходов – системы мгновенно изменяемые (МИС). Кроме того, в результате кинематического анализа выясняется, как именно предстоит рассчитывать систему – достаточно ли для определения усилий в системе одних только  уравнений статики (в случае статически определимой системы) или необходимо рассматривать все три стороны задачи расчёта деформируемой системы – статическую, геометрическую и физическую (если система статически неопределимая). 

Принципиальная схема кинематического анализа приведена на рис.1.6. Методика и техника выполнения проверок, обозначенных на блок-схеме операторами 1, 2 и 3, будут рассмотрены далее. Формально  процедуры, описанные в правой части схемы, могут и не выполняться, если не ставить задачу добиться всё-таки возможности выполнить расчёт сооружения – либо путем трансформации расчётной схемы, либо – для мгновенно изменяемой системы – выбором специальных методов расчёта.

Рис.1.6

Строительная механика рассматривает геометрически неизменяемые системы (сооружения), то есть такие, перемещения точек которых возможны только в результате деформации системы.

Наипростейшей неизменяемой системой является шарнирный треугольник (рис.1.7).

Рис.1.7

Шарнирно-стержневой прямоугольник АВСД, показанный на рис.1.8, является геометрически изменяемой системой, так как приходит в движение без изменения длины и искривления стержней даже при бесконечно малых нагрузках.

Рис.1.8

Кроме уже известных понятий «геометрическая неизменяемость» (и соответственно геометрически неизменяемая система – ГНС), «геометрическая изменяемость» (геометрически изменяемая система – ГИС), «мгновенная изменяемость» (мгновенно изменяемая система – МИС), базовыми понятиями кинематического анализа являются диск, связь и степень свободы.

Д и с к – часть системы (один или несколько соединённых друг с другом элементов), форма и размеры которой могут изменяться только вследствие деформации материала.

Иными словами, если использовать гипотезу отвердения материала (считать материал недеформируемым), то признаком диска будет неизменность формы и размеров.

Рис. 1.9

Примеры дисков приведены на рис. 1.9:

– а, б, в, г, д – диски из одного элемента (а, б, в – стержни с прямолинейной, криволинейной и ломанной в плоскости или в пространстве осью; г – диск-пластинка; д – диск-оболочка);

– е, ж, з, и, к – диски из нескольких элементов (е, ж, з – из однотипных элементов – стержней, плоские (е, ж) и пространственный (з);  и, к – комбинированные пластинчато- и оболочечно-стержневые, пространственные).

Незакреплённый диск может перемещаться в плоскости или пространстве, при этом координаты его точек в общей (глобальной) системе координат xyz изменяются (рис. 1.10), но в собственных (локальных) координатных осях x_D y_D z_D , связанных с самим диском, положение его точек остается неизменным, если считать элементы диска недеформируемыми, – это означает, что диск перемещается как жёсткое целое.

Рис. 1.10

Диск может быть образован соединением нескольких ранее выявленных дисков, имеющих любую (возможно, достаточно сложную) внутреннюю структуру. Пример – на рис. 1.11, где в состав плоского диска I (D_I) входят многостержневые «суб»-диски 1, 2 и 3 (D₁ , D₂ иD₃), объединённые в шарнирный треугольник аналогично примерам на рис. 1.9, е, ж. Неизменяемость формы шарнирного треугольника очевидна; в дальнейшем будет дано доказательство этого.

Рис.1.11

Поскольку возможно последовательное «укрупнение» дисков, то ясно, что в ряде случаев (но не всегда!) вся система может рассматриваться, в конечном счете, как диск. 

Особым диском, который используется в кинематическом анализе, является диск «земля», представляющий собой единую модель всех реальных объектов, играющих роль основания для рассчитываемого сооружения, – фундаментов, других конструкций, поддерживающих рассматриваемую систему.

Диск «земля» всегда считается неподвижным и недеформируемым (возможная деформативность реального основания изначально закладывается в расчётную схему сооружения путем введения податливых опор).

Для обеспечения геометрической неизменяемости сооружения его элементы и более крупные фрагменты (по терминологии кинематического анализа – диски) должны быть соединены (связаны) друг с другом и хотя бы некоторые из них – обязательно с «землей». Соответствующие соединительные устройства принято называть связями. Более общее определение связей объединяет их механико-математическое и прикладное (инженерное) истолкования: 

с в я з и  (механические)  –  ограничения  на  перемещения (линейные  и/или  угловые)  точек  или сечений элементов системы, а также устройства, технически реализующие эти ограничения.

 З а м е ч а н и е :  здесь термин «сечение элемента» не означает разделения  элемента на части, а используется в том же смысле,

как в общепринятых выражениях «гипотеза плоских сечений», «угол поворота сечения», т.е. как   указание на геометрический объект, для которого определяются или описываются кинематические свойства или параметры, в частности, перемещения.

Ограничения (одно или одновременно несколько) перемещений точки или сечения возникают в том случае, когда эта точка (сечение) некоторым способом соединяется с другими точками (сечениями элементов) одного и того же или разных дисков, в том числе диска «земля».

Абстрагируясь от конструктивных особенностей соединительных устройств, будем рассматривать их расчётные модели, применяя к ним в дальнейшем термин «связи».

Классификация связей

Связи различаются по следующим основным признакам:

1) по области расположения – 

а) континуальные – распределённые по объему, поверхности или линии;

б) дискретные –  в отдельных точках или сечениях;

Примерами распределённых связей могут служить деформируемое основание – для лежащих на нем балок, пластин, оболочек, вода – для подводных или плавучих сооружений, воздух – при колебаниях высотных объектов; в дальнейшем ограничимся  рассмотрением только дискретных связей;

2) по соединяемым дискам связи подразделяются  на

а) внутренние –  соединяющие диски системы  друг с другом;

б) внешние (опорные) –  прикрепляющие  диски  системы к диску «земля»;

3) по числу ограничиваемых перемещений выделяют связи 

а) простые (признак – связь накладывает ограничение на одно перемещение);

б) сложные (ограничивается более одного перемещения);

Простые связи различают по типу того одного перемещения, на которое связь накладывает ограничение – линейные и угловые;

4) по физическим свойствам связи бывают

а) жёсткие (недеформируемые);

б) податливые (деформируемые).

Особое значение имеет классификация связей по кинематическому признаку – она будет дана отдельно.

                                            Типы связей плоских систем

Подробно рассмотрим основные типы дискретных связей плоских систем, не делая различия между связями внешними и внутренними, поскольку для самих связей безразлично, какие диски ими соединяются (при этом диск «земля» принципиально   ничем не отличается от прочих дисков системы).

Типы связей устанавливаются по 3-му признаку приведенной выше классификации:

– связи 1-го типа – простые (одно ограничение на перемещения в месте наложения связи) –

а) линейная связь  (рис. 1.12)  – жёсткий  прямолинейный стержень АВ с шарнирами по концам, устраняющий  возможность  относительного (взаимного) линейного  перемещения точки А диска D₁ и точки В диска D₂  по  направлению  оси связи (линии АВ);

Рис.1.12

б) угловая связь  (рис. 1.13, а)  в  виде недеформируемого стержня   А'CВ', объединённого с двумя идеальными (без  трения)  «ползунами»,  жёстко прикреплёнными  соответственно к  дискам D₁ и D₂  в  точках А и В  и  не препятствующими  линейным пере мещениям точек  А и В  вдоль осей ползунов  (а значит, и полному взаимному  линейному  перемещению точек  А и В), но не допускающими относительного (взаимного) поворота узлов или сечений дисков-стержней в точках А и В (если деформации дисков не учитываются, то невозможен взаимный поворот дисков в целом);  на рис. 6, б показано упрощённое изображение внешней угловой связи (когда диском 2 является «земля»); 

Рис.1.13

– связи 2-го типа – шарниры (два ограничения на перемещения в месте наложения связи) –

а)  идеальный (без трения)  цилиндрический шарнир (рис. 1.14) с осью вращения, проходящей через точку С перпендикулярно плоскости, в которой расположены диски D₁ и D₂; цилиндрический шарнир допускает относительный (взаимный) поворот дисков  D₁ и D₂вокруг их мгновенного взаимного центра вращения – точки С, но устраняет возможность любых  (т.е. одновременно,  например, вертикального  и  горизонтального)  относительных линейных перемещений  точек  дисков D₁ и D₂, через которые проходит ось шарнира;

Рис.1.14

б) идеальный (без трения) поступательный шарнир (рис. 1.15) – устройство, состоящее из недеформируемого штока АВ', жёстко прикреплённого к диску D₁ , и направляющей (втулки), закреплённой в точке В диска D_2 ;  поступательный шарнир  позволяет  точкам  А и В, принадлежащим соответственно дискам D₁ и D₂ , совершать свободное линейное относительное  перемещение  вдоль оси шарнира  (линии АВ),  но не допускает  относительного  линейного перемещения точек А и В  по нормали к линии АВ и взаимного поворота узлов (сечений) в точках  А и В  (или взаимного поворота жёстких дисков в целом);

Рис.1.15

– связь 3-го типа – припайка (три ограничения на  перемещения  в  месте наложения связи) – жёсткое соединение дисков (рис. 1.16), полностью устраняющее возможность любых (углового и линейных) относительных перемещений в точках А и В   соединяемых дисков.

Рис.1.16

Сложные связи 2-го и 3-го типов формально могут рассматриваться как различные комбинации простых связей, обеспечивающие соединение дисков, кинематически эквивалентное соответствующей сложной связи (т.е. с такими же ограничениями на взаимные перемещения дисков). Например, цилиндрический шарнир (рис. 1.17, а) эквивалентен двум линейным связям 1-го типа, каждая из которых одним концом прикреплена к одному из дисков (D₁ на рис. 1.17, б) в точках А и В, а другим – ко второму диску (D₂) в общей точке С.

Рис.1.17

Поступательный шарнир (см. рис. 1.15) эквивалентен соединению дисков также двумя линейными связями – параллельными друг другу и ортогональными оси поступательного шарнира (рис.1.18, а).

     

Рис.1.18

На рис. 1.18, б – д показаны различные варианты изображения поступательных шарниров, удобные для использования в расчётных схемах стержневых систем в часто встречающихся случаях, когда оси соединяемых прямолинейных стержней образуют единую прямую, а криволинейные имеют общую касательную в месте соединения. На рис. 1.18, б, г изображены шарниры с осью, совпадающей с продольными осями прямых стержней или с касательной к оси криволинейных стержней – такие шарниры называются продольными поступательными шарнирами. Оси шарниров, показанных на рис. 1.18, в, д, направлены по нормали к осям соединяемых стержней – это поперечные поступательные шарниры.  

Припайка (см. рис. 1.16)  может быть заменена  тремя  линейными связями бесконечно малых размеров (рис. 1.19), оси  которых не должны сходиться  в одной точке или быть параллельными.

Рис.1.19

И наоборот, некоторые комбинации простых связей могут рассматриваться как соответствующие сложные связи. Так, соединение двух дисков двумя линейными связями (рис. 1.20) может быть отождествлено с цилиндрическим шарниром в точке С пересечения направлений осей связей АC' и BC'',  так как эта точка является мгновенным взаимным центром вращения  дисков  D₁  и  D₂.  Однако  нужно иметь  в  виду,  что если бы  в  точке С  был реальный  цилиндрический шарнир,  то  при отсутствии других связей взаимный поворот дисков вокруг точки С  был бы возможен на любой  конечный угол,  а  не  на бесконечно малый,  как в случае мгновенного центра С, когда его положение изменяется с увеличением взаимного поворота дисков. Поэтому шарнир С, условно эквивалентный паре линейных связей, называется фиктивным  (правильнее было бы использовать термин «условный шарнир»).

Рис.1.20

Аналогично пара параллельных линейных связей (рис. 1.21) кинематически эквивалентна фиктивному (условному) поступательному  шарниру с осью, перпендикулярной осям связей  АC'  и  BC''.  Изображение  этого шарнира  не даёт  никаких упрощений, но использование знания его свойств может быть полезным при выполнении кинематического анализа системы. Заметим, что соединения дисков, показанные на рис. 1.20 и 1.21, отличаются только  взаимным  расположением  линейных связей  –  во втором случае точка пересечения направлений их осей удалена в бесконечность.          

Рис.1.21

В выполненном выше изложении типологии связей плоских систем обсуждались их кинематические свойства. Для полного описания свойств некоторой связи служат её кинематическая и статическая характеристики, первая из которых формулирует ограничения, накладываемые связью на перемещения соединяемых ею объектов, а вторая определяет число и виды составляющих компонентов реакций связи. Согласно принципу двойственности в механике (взаимного соответствия друг другу статических и кинематических величин) каждому ограничению перемещений (кинематическому условию) соответствует статический фактор – реакция определённого вида (сила – если связь препятствует линейному перемещению, или момент – при ограничении углового перемещения).

Сводная информация о типовых связях плоских систем приведена в табл. 1, где показаны варианты изображения связей на расчётных схемах, а также даны их кинематические и статические характеристики. Если один из соединяемых дисков – «земля», то связь – внешняя (опорная); специальные упрощённые изображения даны только для внешней угловой связи и внешнего поступательного шарнира (подвижной защемляющей опоры), в остальных случаях никаких различий в обозначениях внешних и внутренних связей одного типа нет.